Deep Learning and Convolutional Neural Networks for Computer Vision

Inside the convolution and pooling layers of a CNN

Why do we use the biological concept and term “neural network” in solving real-time problems within artificial intelligence?

In an experiment with cats in the mid-1900s, researchers Hubel and Wiesel determined that neurons are structurally arranged so that some fire when exposed to vertical edges and others fire when exposed to horizontal or diagonal edges. The concept of specialized components for specific tasks is the basis for convolution neural networks (CNNs) in solving problems like face recognition or object detection from an image.

Convolution and filters

Convolution is the operation of two functions that result in a third function and a resulting output function. It is achieved by extracting the features from an image at different levels. A feature can be edges, curves, straight lines or any similar geometric characteristic.

CNNs use filters — essentially, arrays of numbers — for feature identification. A filter should have the same depth as its input; so, a 6×6 array representing an image should have a 6×6 filter. Filters are also called neurons or kernels.

Consider this illustration of using a filter in a CNN for feature recognition. The sample filter below detects a straight line in an image:

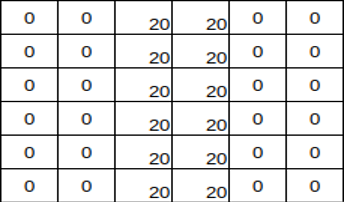
Filter for detecting straight lines

In the images below, that same filter is applied to two different images.

The first image contains a hand-drawn line — the numeral 1 — and an array representing it:

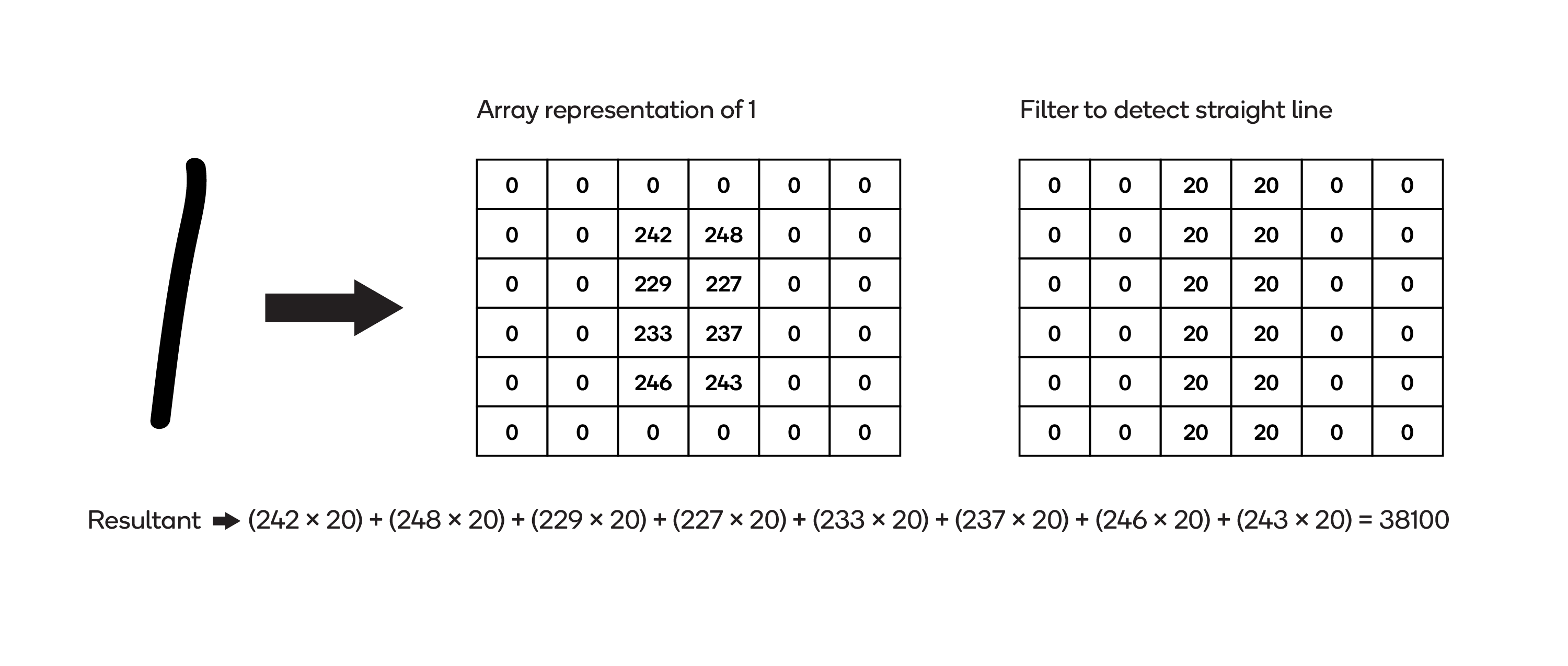
Applying filter to an image with straight lines

The sum of the products of the two arrays (the “resultant”) is 38,100.

The next image contains a hand-drawn numeral 2 — not a straight line — and an array representing it:

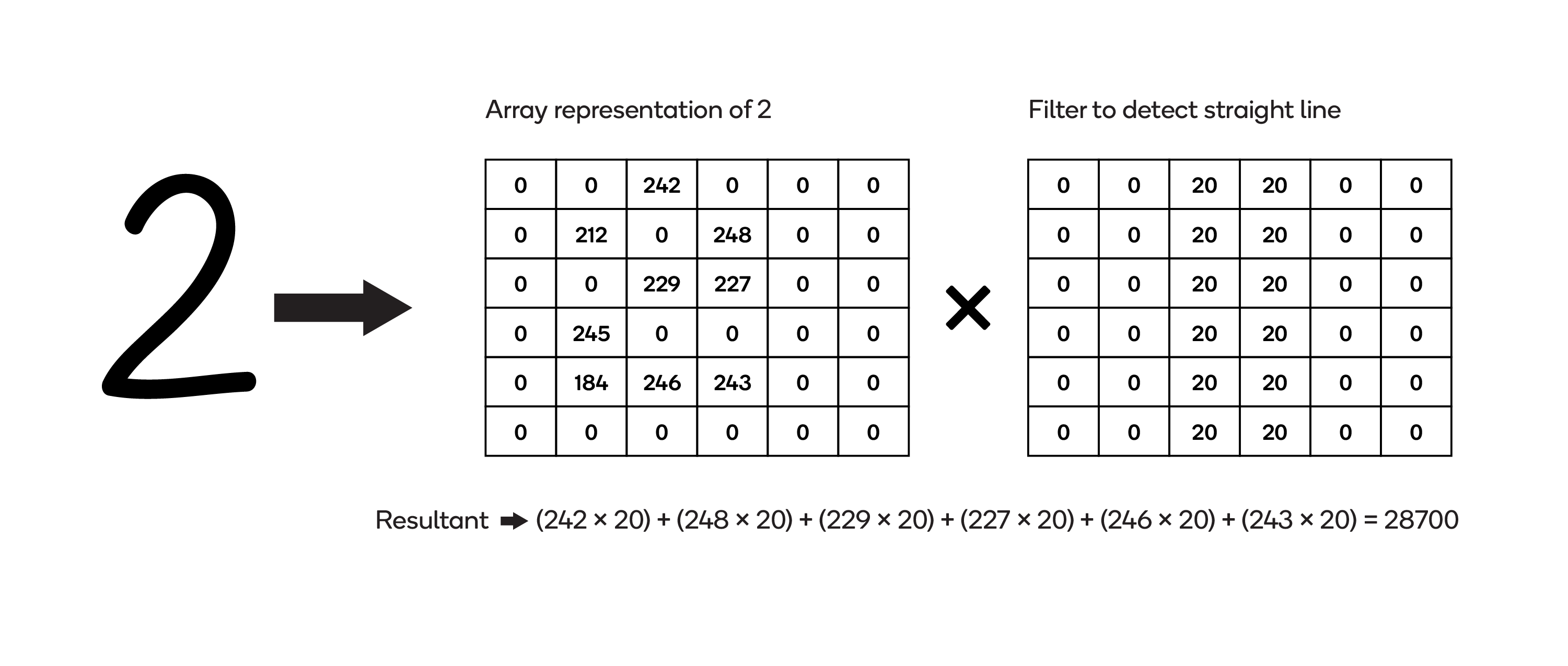
Applying filter to an image without straight lines

Fewer of the non-zero entries in the array align with those in the filter, so the resultant — 28,700 — is much lower than in the first image.

That illustrates filtering in a CNN. The image below depicts the architecture of a sample convolutional neural network.

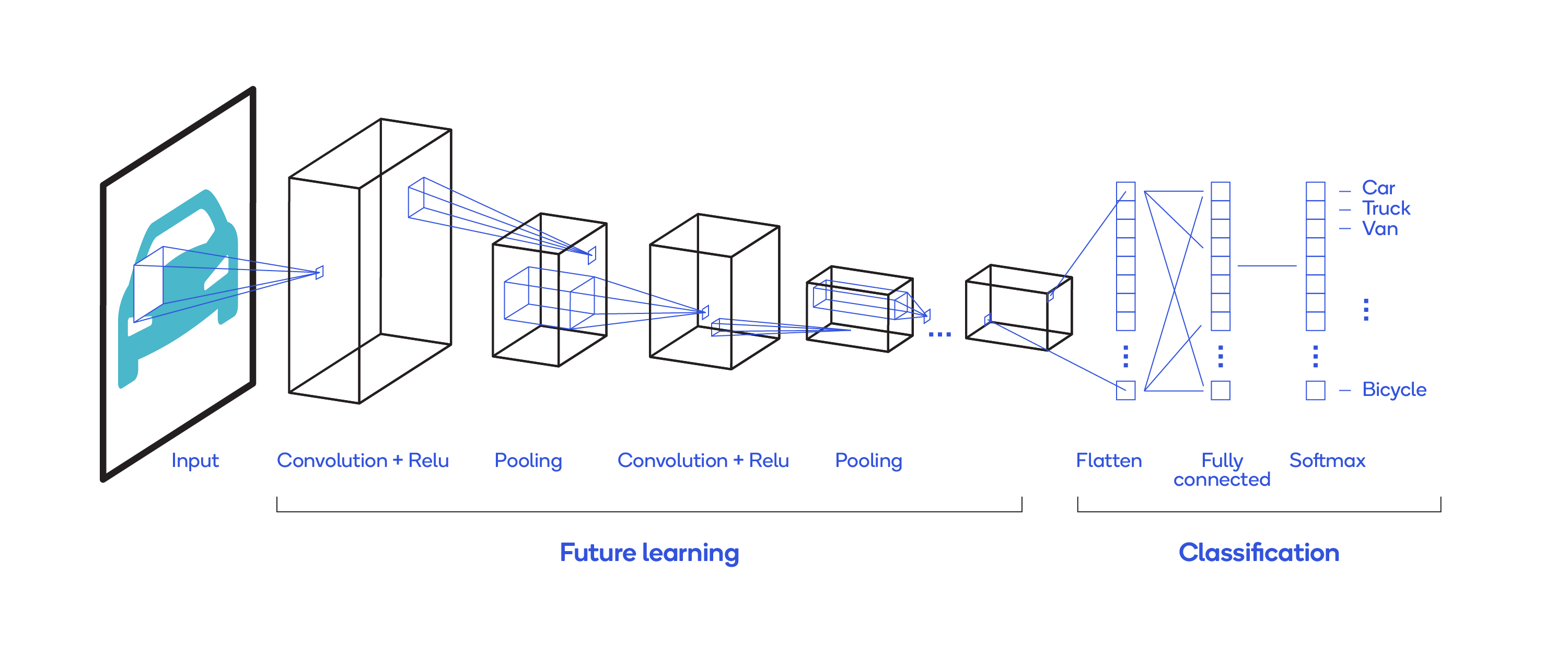
CNN Architecture

Following are terms commonly used in describing CNNs.

Activation

Activation is the function used to get the output of a node in the neural network. In CNNs, activation functions indicate linearity or non-linearity of the results. They map the resultant to either (0, -1) or (-1, 1). Commonly used activation functions are sigmoid, tanh and Relu.

Feature map

The resultant of the convolution process is called a feature map. Shown below is a formula to calculate the dimensions of the output of a convolution operation:

• An image matrix (volume) of dimension (h × w × d)
• A filter (f_h × f_w × d)
• Outputs a volume dimension (h – f_h + 1) × (w – f_w + 1) × 1

Stride

Stride describes the number of positions by which the kernel is moved over an image, horizontally and vertically, to perform a complete convolution operation.

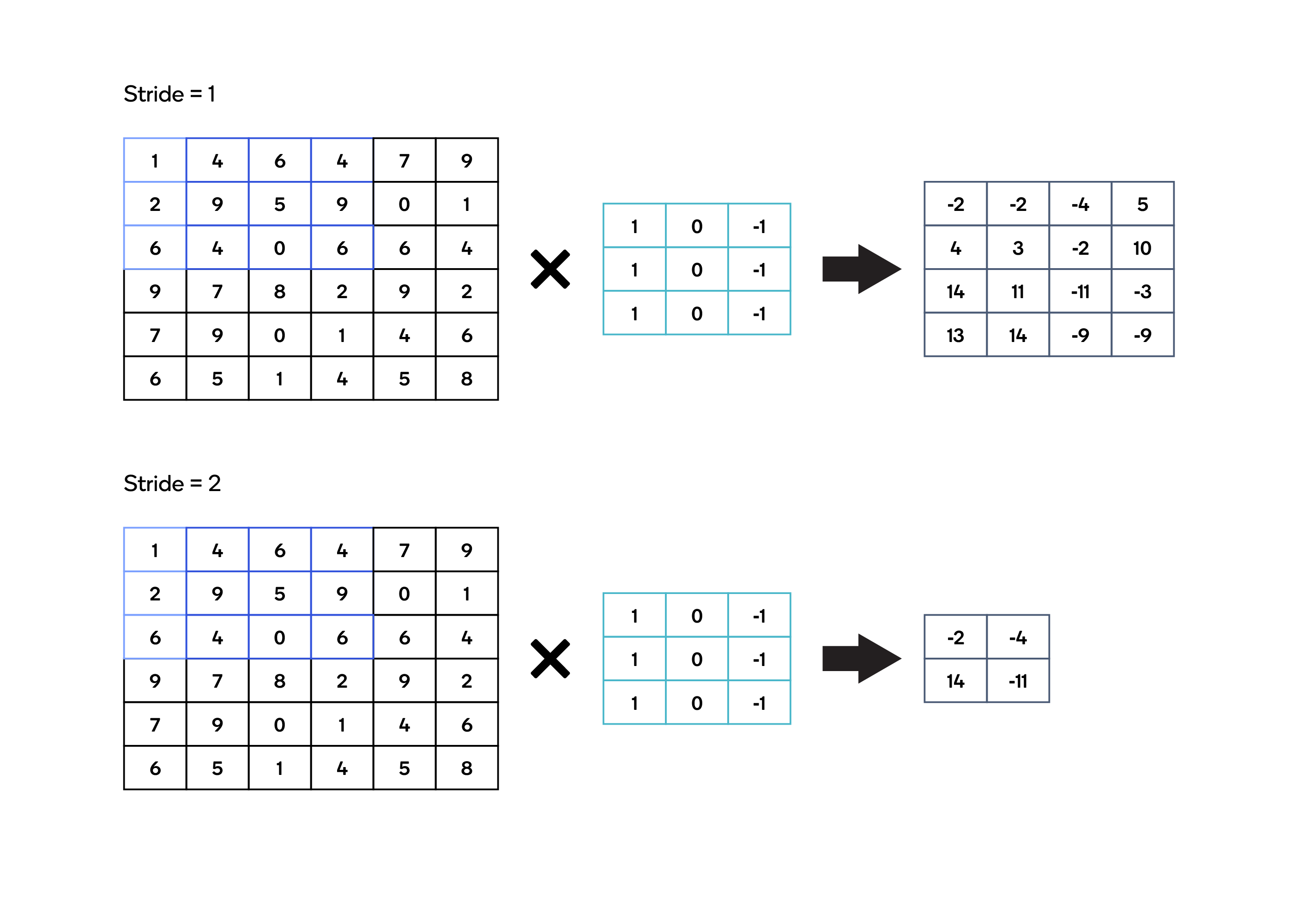
Stride

Pooling

Pooling is used to reduce the spatial size of the representation. It is performed on the feature map.

Max pooling and average pooling are the most commonly used pooling methods. The pooling operation is performed next to the convolution operation to reduce the input size of the representation before the representation goes to the next layer.

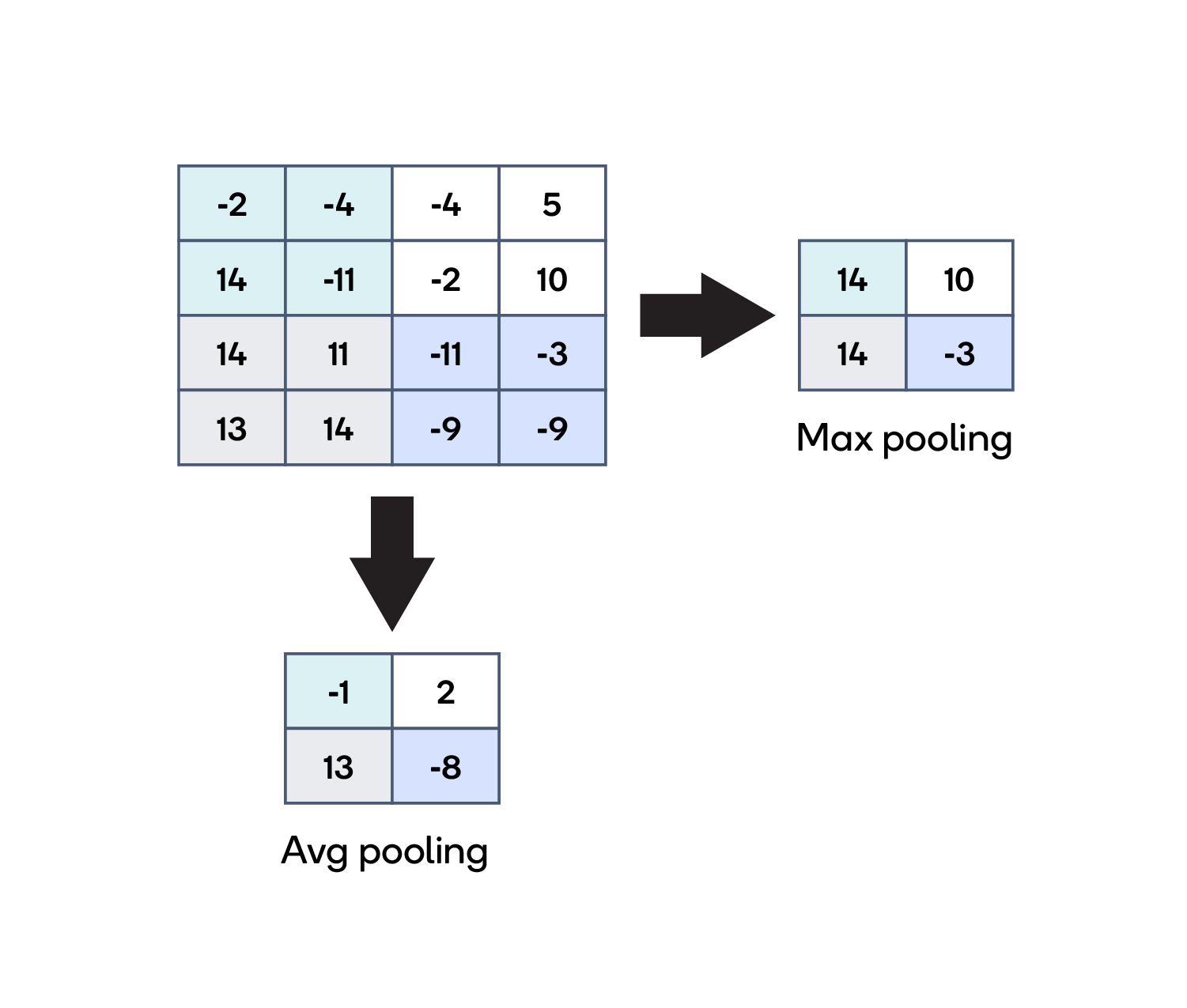
Pooling in CNN

Flattened layer

A flattened layer is used to convert the n-dimensional vector into a mono-dimensional vector. In our case, we convert a structured, two-dimensional image into a mono-dimensional vector, which is the input layer for the neural network.

Fully connected layer

A fully connected layer connects each neuron of one layer to every neuron of another layer. The last layer of the fully connected layer is given for an activation function so that it can be helpful in classification.